Why monarchs are an enzyme – Part 1
Monday, February 10th, 2020 at 7:11 am by Chip TaylorFiled under Monarch Biology | Comments Off on Why monarchs are an enzyme – Part 1
Monarchs are an enzyme or rather a complex set of enzymes that interact with the physical environment in a deterministic manner. In this article, I’m going to argue that the responses of monarchs to physical conditions are determined by their genetic code which defines metabolic processes that are mediated by enzymes and biocatalysts that respond in predictable ways with the physical environment. Enzymes, as you may recall, are mostly proteins that mediate reactions with substrate molecules yielding products that mediate cellular and metabolic processes that sustain life. These processes are rate-limiting which means they are a product of the quantities of the enzymes, the substrates and temperature (and sometimes pH). Since insects, and most invertebrates, are cold blooded, with few exceptions, it is the ambient temperature that governs these reactions and ultimately the responses of the organisms to the physical conditions.
Specifically, I’m forwarding the view that an understanding of the range of responses by monarchs to a variety of conditions will help us understand and predict the inter-annual variation in monarch numbers. While the following may be obvious to some readers, conversations with colleagues suggest that many do not understand or agree with my interpretations. That said, hear me out and see what you think.
The underlying thesis is that the monarch’s DNA defines a set of limits and optima for each monarch as it interacts with the physical and biological environment. I wasn’t great at biochemistry but was impressed by enzyme kinetics and all the cascading results. Enzymes mediate chemical interactions deterministically, and in simple laboratory systems in which quantities of the interacting components are held constant, it is clear that each reaction is defined by temperature and pH with a lower limit or zero point at which no reaction is catalyzed, a rise in activity as temperatures increase, an optimal temperature for interaction with the substrate and then a decline as temperature increases even further to an upper limit where again reaction with the substrate reaches zero (Fig 1).
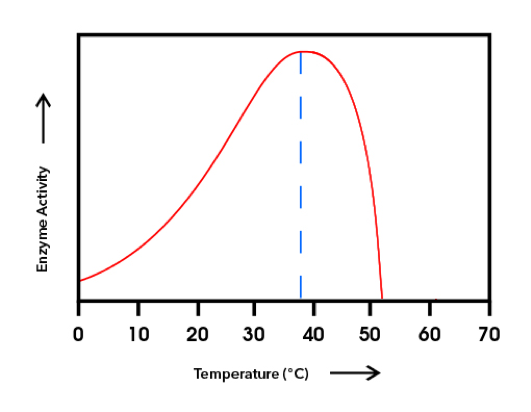
Figure 1. A generalized enzyme activation curve. The degree day model for the development of monarch larvae developed by Zalucki (1982) indicates a developmental zero of 11.5°C (52.7°F) at the lower extreme, an optimal temperature of 29°C (84.2°F) and an upper developmental zero of 33°C (91.4°F).
Living systems are complex with lots of enzymatic interactions having different optima and with lots of complex rate limiting interactions as well but, in my view, within the organism, all these interactions are deterministic as opposed to stochastic or random*. If you are with me so far, the argument is that the DNA driven and limited biological engine represented by the monarch functions at rates determined by temperature, light, sometimes humidity, and more rarely the composition of the surrounding gases. There are biological factors such as host plant quality, predators, pathogens and parasites to consider, and all of these respond to physical factors as well. Overall, the response to physical factors, particularly temperature, by all the biological components of the monarch ecosystem appears to be the driver that broadly determines monarch breeding success during a given year. In effect, they determine realized fecundity, a subject that I’ll deal with in Part 2.
It follows that to fully understand inter-annual variation, and to sort out the effects of biological factors, we need to define the deterministic properties of the monarch system. We can call them physical windows within which the organism functions – as an example, imagine a range of temperatures with death due to freezing at one end and death due to extreme heat at the other. Monarchs function between these limits. There is a lower limit for growth and upper limit for growth. These limiting temperatures are known as developmental zeros. For caterpillars, the low point is 11.5°C (52.7°F) and the high point is 33°C (91.4°F). At either of these extremes, caterpillars stop feeding and the metabolic system slows down. If these temperatures are maintained for long periods, the caterpillars will run out of the enzymes, metabolites and blood sugars necessary to keep the systems going and will die. There is an optimal temperature for growth as well. If we find a fifth instar caterpillar in the wild, we can estimate how long it has been a caterpillar, if we know the temperatures the caterpillar has experienced over the last two weeks or more. The calculation is based on a degree day model which, to me, is effectively an enzyme kinetic model. What I’m arguing is that we extend the degree day model to all of the other physical factors to which monarchs are exposed.
Example windows include an ambient light window, a temperature window (for all flight and for the migration specifically – and they are different), a wind speed and direction window (again with variation depending on reproductive vs migratory status), a thermal window for gliding and soaring, an oviposition window, a mating window, an e-factor window (polarization) and a few more.
Basically, we need to know how monarchs spend their days under a variety of physical conditions – the window (time, temp, light, etc.) for oviposition would be one of my first targets. I want to understand the optimization functions in the system.
Over the last 10 years or so I’ve spent many hours trying to assess the impact of physical factors on the yearly growth of the monarch populations. We focused mostly on temperature and the regressions indicated there were strong associations between temperatures in Texas in March and April and the development of the population each year. However, the regressions only explained about 40% of the year to year variation. Clearly, there was something missing. I eventually realized that mean temperatures, or rainfall, or drought indexes, were only surrogates for what was really happening. After plotting data for yet another regression, I recognized that the outcome represented an optimizing function rather than a linear relationship, and that we needed to understand the system in terms of a series of linked optimizations. Once that became clear, it was evident that, if we knew the optima for a variety of factors and could associate those with monarch specific distributions and reproductive output, we could derive a predictive model to explain monarch numbers both regionally and for most of the eastern monarch population. I have been using a crude optimization model for the last several years to predict the population trends. Some of my predictions based on this approach have been short of my expectations and others have been on the mark. It’s an iterative process of learning from my mistakes and successes.
There are many more aspects to this theme such as how this interpretation relates to behavior of individuals with specific genotypes, realized fecundity, population crashes and perhaps even to the insect apocalypse. I’ll provide additional explanations and examples in Part 2.
Here is a departing observation: in 9/11 years during which the mean temperature for March in Texas was greater than 1.9°F above the long-term average the population declined. However, for each of the 4 years with March mean temperatures <-1.5°F, the population increased. What did enzymes and optimization functions have to do with those outcomes? Plenty, as I will explain in Part 2. [Edit: Why monarchs are an enzyme – Part 2 is now online.]
*Monarch populations are defined by stochastic events to be sure but, I will argue that much of the mortality experienced during many of these events is determined by genetic limitations.
Reference
Zalucki, M.P. (1982), TEMPERATURE AND RATE OF DEVELOPMENT IN DANAUS PLEXIPPUS L. AND D. CHRYSIPPUS L. (LEPIDOPTERA:NYMPHALIDAE). Australian Journal of Entomology, 21: 241-246. doi:10.1111/j.1440-6055.1982.tb01803.x


Sorry, comments for this entry are closed at this time.